怎么理解支持向量机SVM算法这一概念及其应用场景?这篇文章里,作者做了相对详细的分析和解读,一起来看一下。

一、什么叫支持向量机算法
支持向量机SVM算法,英文全称是“Support Vector Machine”。在机器学习中,SVM是监督学习下的二分类算法,可用于分类和回归任务。
二、基本原理
SVM的核心任务就是:构建一个N-1维的分割超平面来实现对N维样本数据放入划分,认定的分隔超平面两侧的样本点分属两个不同类别。我们还是从一个最为简单的示例开始讲起(二维平面):
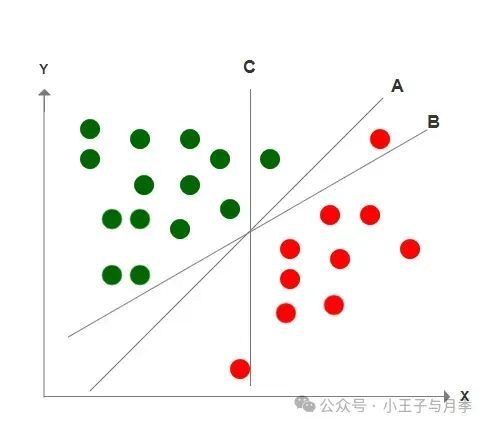
情况1:请大家观察一下,A、B、C三条直线哪一条才是正确的分类边界呢?显而易见,只有A“完整”的区分了两种数据的决策边界。
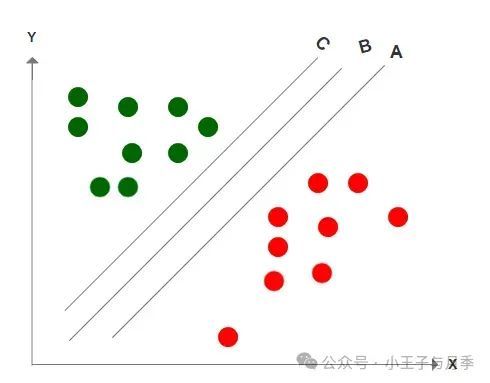
情况2:与情况1不同的是,上图中,A、B、C三条线都完整的区分了边界,那我们应该如何选择呢?既然能分豆的工具这么多,那我们理所当然应该找一个最好的是不是?最佳答案应该是B,因为B与边数据的距离是最远的,之所以选择边距最远的线,是因为这样它的容错率更高,表现更稳定,也就是说当我们再次放入更多的豆的时候,出错的概率更小。
那么由此推导出,SVM的分类方法,首先考虑的是正确分类;其次考虑的优化数据到边界的距离。接下来更麻烦的情景出现了,请看下图,这堆豆子要怎么分?如果这是在一个二维平面上,这些豆子应该用一条什么线来划分呢?
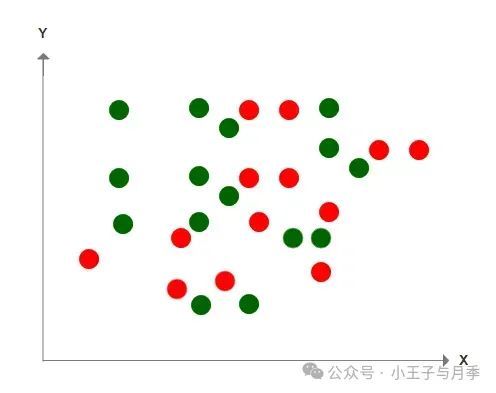
难道我们真的要在画一条无限曲折的线去划分吗?如果再怎样曲折还是无法区分又该怎么做呢?这就是线性不可分的情况,其实在现实生活中,大量的问题都线性不可分,而SVM正是处理这种线性不可分情况的好帮手。
处理这类问题的办法就是,将二维平面转化到一个三维空间,因为往往在低维空间下的非线性问题,转化到高维空间中,就变成了线性问题。比如说上面的图也许就变成了下方的情况。
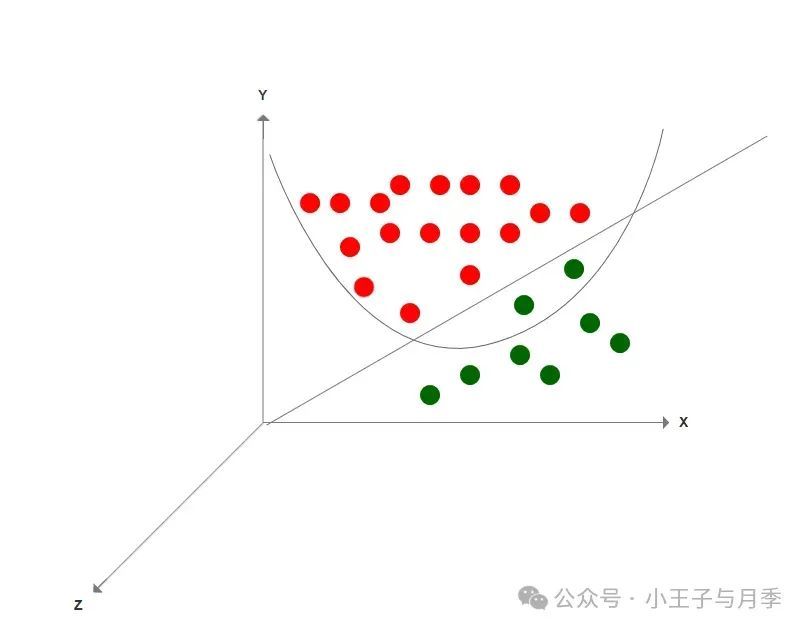
如上图所示,即三维样本数据被二维平面划分,在二维空间中的不可分问题也被转换成了三维线性可分问题,可以被支持向量机处理。基于这个思想,SVM采用核函数来实现低维空间到高维空间的映射,从而在一定程度上解决了低维空间线性不可分的问题。
下面我们简述一下关于核函数的定义,以利于进一步理解他的作用。
核函数:任意两个样本点在扩维后的空间的内积,如果等于这两个样本点在原来空间经过一个函数后的输出,那么这个函数就叫核函数。作用:有了这个核函数,以后的高维内积都可以转化为低维的函数运算了,这里也就是只需要计算低维的内积,然后再平方。明显问题得到解决且复杂度极大降低。总而言之,核函数它本质上隐含了从低维到高维的映射,从而避免直接计算高维的内积。
常用的核函数有如下一些:例如线性核函数、多项式核函数、径向基核函数(RBF)、高斯核函数、拉普拉斯核函数、sigmoid核函数等等。三、支持向量机算法的应用步骤
下面是SVM算法应用过程中的关键步骤:
第一步:数据准备与预处理(通用)在应用SVM前,首先需要收集并准备相关数据。数据预处理步骤可能包括数据清洗(去除噪声和不相关的数据点),数据转换(如特征缩放确保不同特征在相近的数值范围),以及数据标准化处理。
第二步:选择核函数根据数据集的特性选择合适的核函数,是SVM核心的步骤之一。如果数据集线性可分,可以选择线性核;对于非线性数据,可以选择如径向基函数(RBF)核或多项式核来增加数据维度并发掘复杂的数据关系。
第三步:参数优化优化SVM的参数(例如C参数和核参数)对模型的性能有着直接的影响。C参数决定数据点违反间隔的程度的容忍性,而核参数(如RBF核的γ参数)控制了数据映射到高维空间后的分布。
第四步:训练SVM模型使用选定的核函数和优化后的参数,利用训练数据来训练SVM模型。在这个阶段,算法将学习划分不同类别的最佳超平面,并确定支持向量。
第五步:模型评估(通用)利用测试集来评估SVM模型的表现。常见的评估指标包括准确率、召回率、F1分数等。评估结果可以帮助我们了解模型在未知数据上的泛化能力。第六步:模型部署与监控(通用)
最后一步是将训练好的SVM模型部署到生产环境中,并实施持续监控。在模型部署过程中,需要确保实时数据的格式与训练时一致,并对模型进行定期评估以适应可能的数据或环境变化。
四、应用场景
SVM不仅适用于线性问题,还适用于非线性问题,具有较好的分类性能和泛化能力,适用于多种实际问题的解决。
- 文本分类:SVM可以将文本表示为特征向量,并通过训练一个SVM分类器来将文本分为不同的类别,如垃圾邮件分类、情感分析、文本主题分类等。
- 图像分类:通过提取图像的特征向量,可以使用SVM来训练一个分类器,将图像分为不同的类别,如人脸识别、物体识别、图像检索等。
- 生物医学领域:可以使用SVM来进行癌症分类、蛋白质结构预测、基因表达数据分析等。
- 金融领域:SVM可以用于金融领域的多个任务,如信用评分、欺诈检测、股票市场预测等。
- 医学图像分析:可以使用SVM来进行病变检测、疾病诊断、医学图像分割等。
- 自然语言处理:可以使用SVM进行命名实体识别、句法分析、机器翻译等任务。
五、优缺点
优点:
- 效果很好,分类边界清晰;
- 在高维空间中特别有效;
- 在空间维数大于样本数的情况下很有效;
- 它使用的是决策函数中的一个训练点子集(支持向量),所以占用内存小,效率高。
缺点:
- 如果数据量过大,或者训练时间过长,SVM会表现不佳;
- 如果数据集内有大量噪声,SVM效果不好;
- SVM不直接计算提供概率估计,所以我们要进行多次交叉验证,代价过高。
参考:
本文由@厚谦 原创发布于人人都是产品经理,未经作者许可,禁止转载。
题图来自Unsplash,基于CC0协议。
该文观点仅代表作者本人,人人都是产品经理平台仅提供信息存储空间服务。
友情提示
本站部分转载文章,皆来自互联网,仅供参考及分享,并不用于任何商业用途;版权归原作者所有,如涉及作品内容、版权和其他问题,请与本网联系,我们将在第一时间删除内容!
联系邮箱:1042463605@qq.com